The Birthday Paradox
why we have more in common than we think

I) Surprise!
There was this one class that stuck out during my undergrad. The statistics professor asked a student for his birthday.
He predicted that there is at least more than one person with the same birthday. He asked for a show of hands to a lecture of 200 students. Sure enough, 4 other students raised their hands. 🤯
That has to be a coincidence, right? There’s 365 days in a year. It felt impossible.
That’s the beauty of probability—it defies intuition. It’s mathematics making sense of seemingly random chance.
II) A Crash Course on Collision
Let’s start with the assumptions (see appendix):
365 birthdays in a year1,
The birthdays are equally distributed, meaning that the same number of babies are born each day in any given year.
This is the birthday problem: As the number of people in a room increases, the likelihood of at least 2 people to have a matching birthday increases. It takes a room of 23 people to get to a 50% chance of having at least one pair of shared birthdays—what is known as a collision.
We can test this out in real life. Take the 20 Premier League teams. Each team has over 20 players. We can reasonably expect about half the teams to have a shared birthday.
I took the liberty to test it out and 12 of the teams do have shared birthdays. Some more than others.
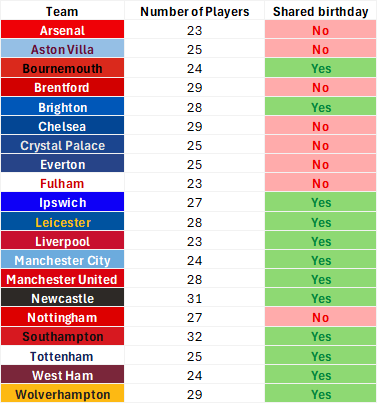
This result should hold in any group—be it a classroom, the office, or any social gatherings.
What’s more, it doesn’t take much to make it certain. Just 57 people, and the likelihood rockets up to 99%.
Why is this so? Because the likelihood of NOT finding a match becomes vanishingly small as groups get larger.
In a sufficiently large group, it is almost impossible to have no one sharing a birthday. Almost.
The math seems crazy, but it works. Our brains are not naturally equipped to deal with probabilities and large numbers. What seems to be an outlier turns out to be a common result.
III) Common Denominator
My point? We have more things in common with each other than not.
Put enough people together in a room, clusters across shared traits naturally emerge—be it interests, values and personality types. Even first names are shared.
There’s 8 billion people on the planet today. We’d like to think we’re all unique in all our ways.
We’re more alike than we think.
Too often, we focus on the differences that don’t matter. Which makes finding people who share our values and interests feel elusive.
But the math suggests that differences rarely overshadow our similarities.. It’s a matter of meeting more people and expanding our social circles. By putting ourselves out there, we take that first step to make meaningful connections.
Unlike birthdays, which are set, we can adapt our interests and work on ourselves—increasing our surface area for luck. Improving our chances to find others, and others to find us.
What’s more, there’s the internet and online platforms. They’re driven by algorithms built to connect us based on shared interests, They’re powerful tools when used wisely.
IV) Matchmaker
The math is clear. More people, More connections.
It’s called matchmaking, right? It can be made. Serendipity can be set in motion.
Whether you’re looking for a friend, a job, a business partner, or someone to build a life with.
So don’t wait for chance encounters. Put in the work.
Go out, meet people, join a group.
You’ll be surprised by the things you have in common.
Inspirations
1. Laps around the sun
My first post on substack was about birthdays. This would be my 30th.
2. The phenomena of Probability Matching by Kris Abdelmessih @ Moontower
3. Dating Data by Kyla Scanlon
4. The One and The Many by Stephen Fry
5. Birthday Problem math
Interesting to note, the first known publication of the birthday problem is by Richard von Mises, brother of the Austrian economist Ludwig von Mises.
appendix
Uniform birthdays
It’s fair to assume a uniform distribution for each day in a year. While we can expect to see some seasonality and variation with births, the data shows that it doesnt vary that much, at least in Malaysia, from 1982 to 2022. Total number of people in that 40 year span, on a given birthdate range from 50,000 to 60,000.
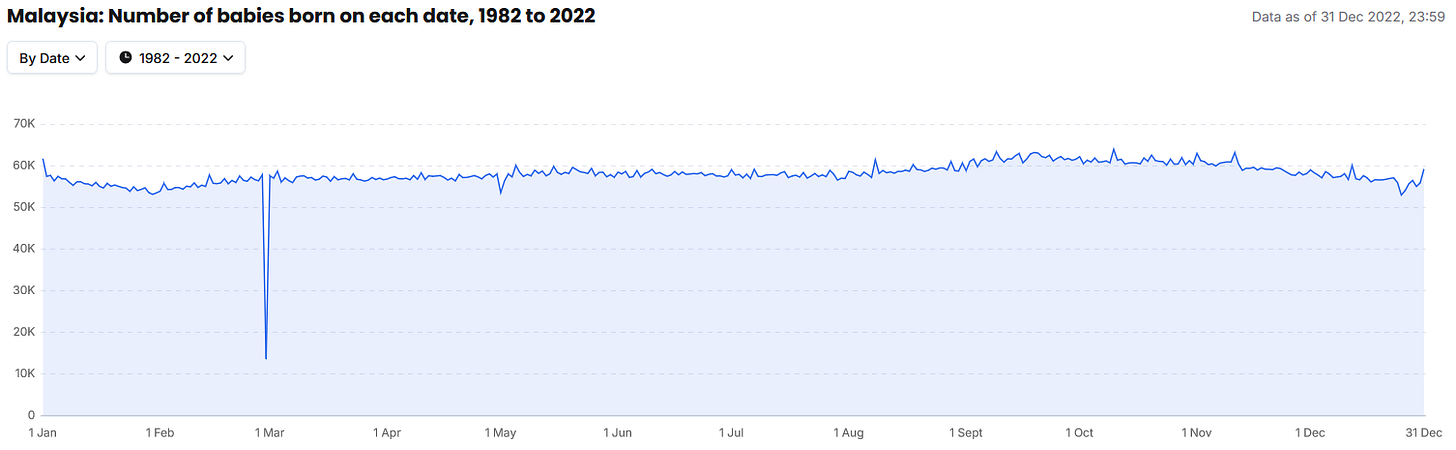
With February 29, the leap day, accounting for about 13,500. Which is a quarter of any other given date. But for the sake of simplifying the math, we ignore them2.
sorry leap year babies.
sorry, not sorry.




